Kerbin itself is a bit smaller than Earth, with a solar system that's similar but with different distances and sizes. Because the hope here is to show in obvious terms how hard orbit is, and also how very expensive it is to send more stuff into space, the absolute difference in sizes should not matter; the relative differences should more than suffice.
 |
| I can't help seeing this and thinking "Missile" |
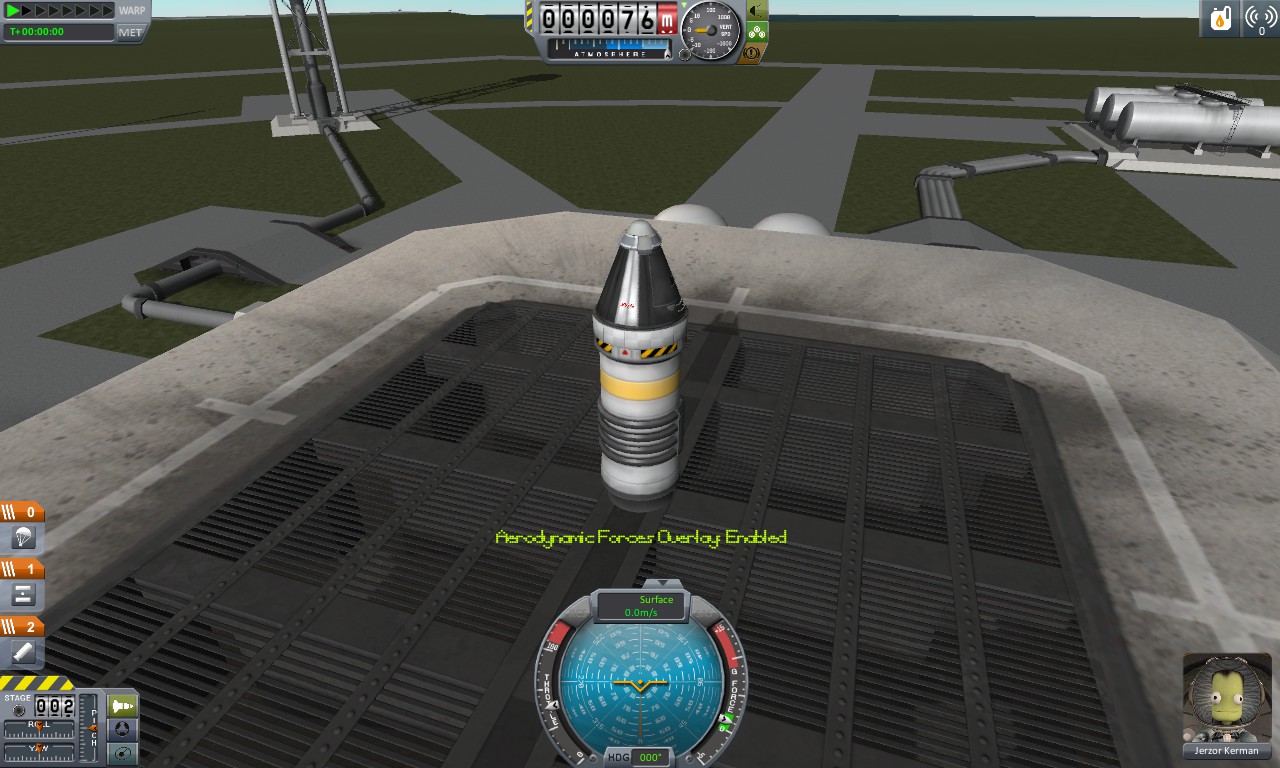
We start off with the simplest craft imaginable. A crew pod, a heatshield, and a parachute, all on top of a single solid-fuel rocket. When talking about rockets, it's usually useful to split the rocket into two parts: the payload, and the rest of the rocket. Here, our payload is everything on top of the rocket, which all weighs 1.2t. (I'm assuming the measurement system is tons). The rocket itself weighs in at 3.56t, (the entire craft weighs 4.9t) with the fuel inside weighing 2.8 tons. For reference, this means 24% of the rocket is the stuff we want in space, 57% of it is fuel, and the remaining 19% is structural mass. Not too bad.
 |
| One guess as to what this rocket reminds me of |
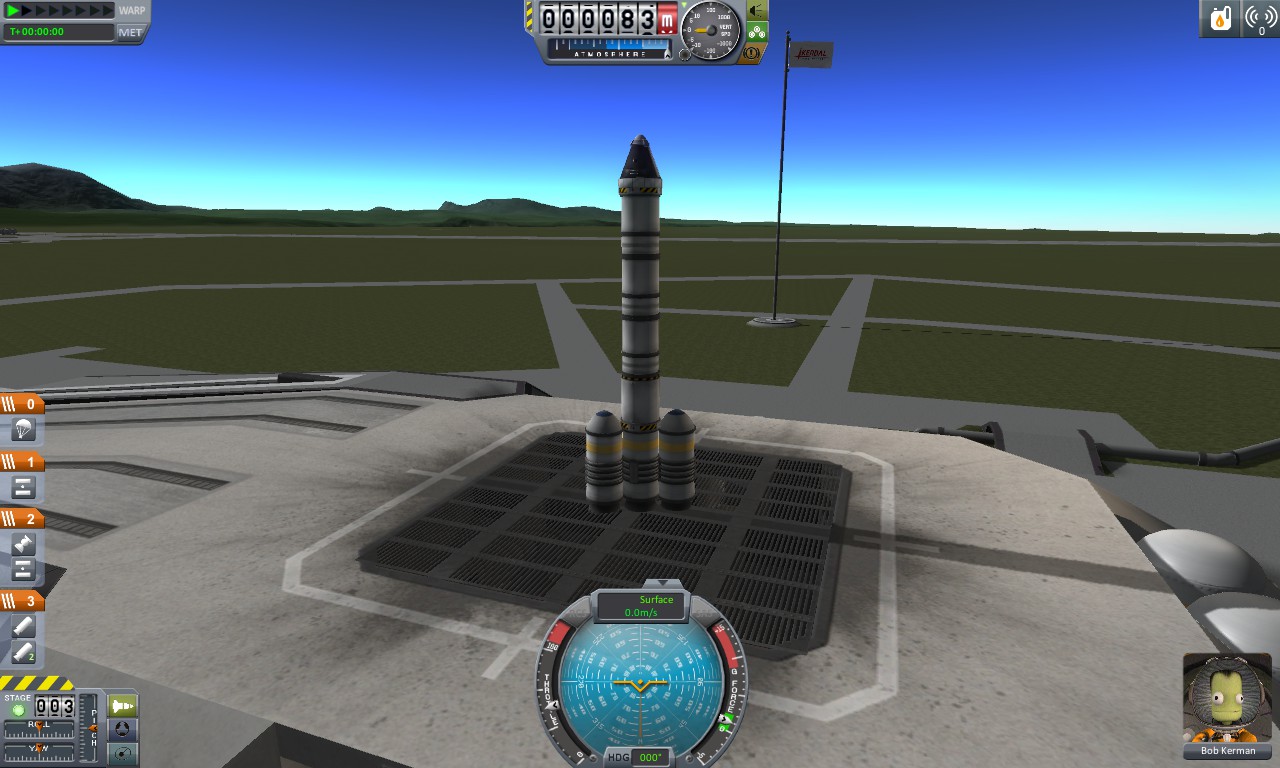
Next up, we have a craft that can get into orbit and come back down. In fact, it has a little extra fuel for emergencies/bad piloting, but not by much. You can see it has the same payload as the first, so 1.2t again is what we want in orbit. The rocket certainly increased in size though; it in total now weighs 20.3t; the entire craft is four times bigger to get something into orbit, rather than getting it up into space. If anyone ever asks, remember that the hard part is going fast enough to get into orbit, not getting high enough.
Our rocket now has two stages; a bottom stage with three of the same solid-fuel rockets we used in the original rocket, and a second liquid-fuel rocket stage. For reference: the first stage weighs 10.68t, with 8.4t of that being solid fuel. The second stage weighs 8.25t, 6.3t of which is fuel and oxygen. All told, our rocket is now 6% what we want, 72% fuel, and 22% structure mass for the rocket. If you're thinking that this looks like a bad ratio between fuel to everything else, think again. This is actually fairly normal. Rocketry equations are crazy.
 |
| This is the only design that makes me think "Real Rocket" |
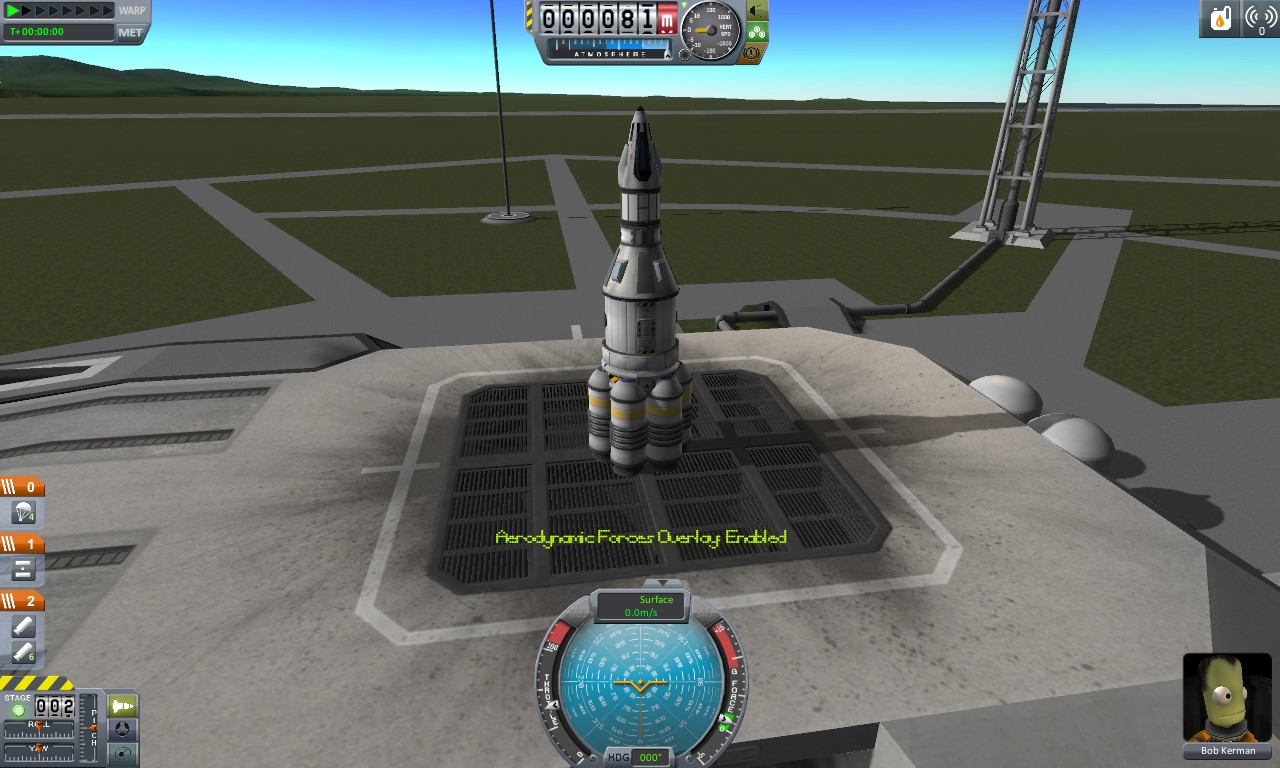
Like the first craft I showed, this one is built only to get to orbital height, but not into actual orbit. Like the first, it also doesn't reach high enough, but the two are close enough to compare. The payload this time weighs in at 5.9t, or about 5 times heavier. Underneath are 7 of the same solid-fuel rocket, weighing 24.92t, with 19.6t spent on fuel. The entire craft weighs 31.4t, and the readout involves 19% payload, 62% fuel, and 17% structure. Note the fun part here: we have a rocket substantially bigger than the first, with a much larger payload, but the ratios are all relatively similar. Given the variance between which heights they reach and how air resistance factors in, these are really rather similar. But will the same occur with an orbital variant?
 |
| While I'd rather have all the rockets at the bottom, it was too unstable |
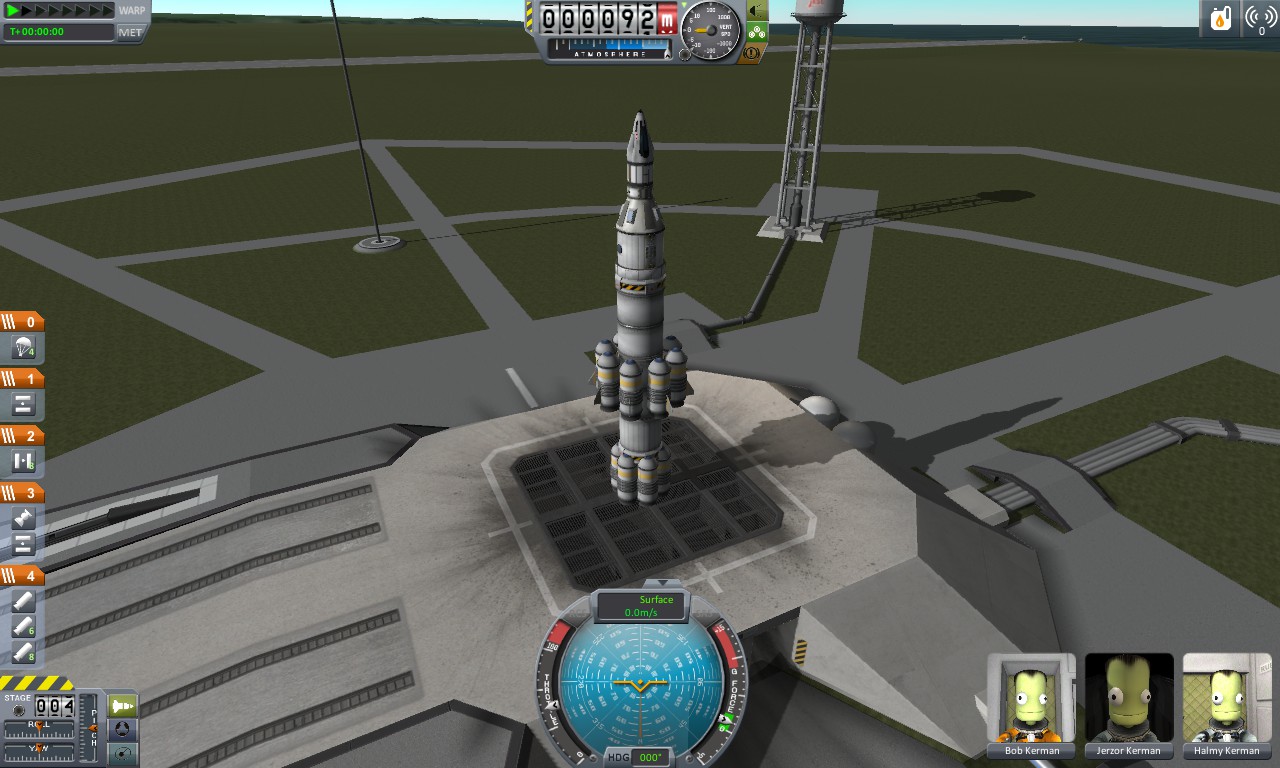
Here's the same payload, but with enough rocket to put it into orbit and come back again. The craft weighs at 99.8t, with the same 5.9t spent on payload. It has 2 stages, one of 15 solid fuel rockets, at 53.4t, and a second liquid fuel stage of 39t. The percentages this time are: 6% payload, 74% fuel, and 20% structural. Unsurprisingly, the ratios are similar to the first orbital rocket!
Even though we had a much larger payload, and a much larger rocket going up, the percentages remained similar. Why? The Tsiolkovsky Rocket Equation. The delta-v required for a given mission will be similar between rockets of various sizes. Assuming they use similar rocket types, they'll have similar exhaust velocities, and so their mass ratios will be similar as well.
Final notes: For anyone familiar with the game, yes, you could make rockets that were likely better than these. I was deliberately attempting to make rockets that behaved similarly to each other, which mandated some inefficiencies. I also used the scientifically less accurate term "weighs" instead of masses, because it sounds better conversationally. Outside of science, one does not refer to mass, they refer to weight, and the word "massive" especially is terrible for conversation. And if you have any questions or comments, please do leave a comment here, and I'll get to it shortly.